题目内容
8.已知圆O:x2+y2=r2与圆C:(x-2)2+y2=r2(r>0)的一个公共点P,过P作与x轴平行的直线分别交两圆于A,B两点(不同于P点),且OA⊥OB,则r=2.分析 根据题意,画出图形,结合图形得出点P的横坐标,再根据题意列出方程组,解方程组求出半径r的值.
解答 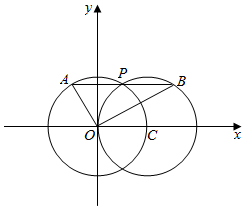 解:如图所示,
解:如图所示,
圆O:x2+y2=r2与圆C:(x-2)2+y2=r2(r>0)的一个公共点P,
∴点P的横坐标为x=1;
又过点P作与x轴平行的直线分别交两圆于A,B两点,
设A(x1,y1),B(x2,y2),则$\left\{\begin{array}{l}{{y}_{1}{=y}_{2}}\\{{x}_{1}{+x}_{2}=2}\end{array}\right.$;
又OA⊥OB,∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=0,
且${{x}_{1}}^{2}$+${{y}_{1}}^{2}$=r2,${{(x}_{2}-2)}^{2}$+${{y}_{2}}^{2}$=r2;
由此解得r=2.
故答案为:2.
点评 本题考查了直线与圆的应用问题,也考查了数形结合解题方法的问题,是综合性题目.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
16.已知函数$f(x)=\frac{4^x}{{{4^x}+1}}$,则f(-2016)+f(-2015)+…+f(-1)+f(0)+f(1)+f(2)+…+f(2015)+f(2016)=( )
| A. | 2016 | B. | 2017 | C. | $\frac{4033}{2}$ | D. | 4033 |
18.i是虚数单位,若$\frac{1+7i}{2-i}$=a+bi(a,b∈R),则a+b的值是( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |