题目内容
16.已知函数$f(x)=\frac{4^x}{{{4^x}+1}}$,则f(-2016)+f(-2015)+…+f(-1)+f(0)+f(1)+f(2)+…+f(2015)+f(2016)=( )| A. | 2016 | B. | 2017 | C. | $\frac{4033}{2}$ | D. | 4033 |
分析 易知f(-x)+f(x)=$\frac{{4}^{-x}}{{4}^{-x}+1}$+$\frac{{4}^{x}}{{4}^{x}+1}$=1,从而求和.
解答 解:f(-x)+f(x)=$\frac{{4}^{-x}}{{4}^{-x}+1}$+$\frac{{4}^{x}}{{4}^{x}+1}$=1,
∴f(-2016)+f(-2015)+…+f(-1)+f(0)+f(1)+f(2)+…+f(2015)+f(2016)
=2016+f(0)=2016+$\frac{1}{2}$=$\frac{4033}{2}$,
故选:C.
点评 本题考查了函数的性质的判断与应用.

练习册系列答案
相关题目
4.在等差数列{an}中,Sn为其前n项和,S7=35,a2+a3+a10=12,则Sn的最大值为( )
| A. | 28 | B. | 36 | C. | 45 | D. | 55 |
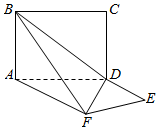 平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.
平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.