题目内容
20.已知等差数列{an}的公差d≠0,且a1,a3,a9构成等比数列{bn}的前3项,则$\frac{{{a_1}+{a_3}+{a_6}}}{{{a_2}+{a_4}+{a_{10}}}}$=$\frac{5}{8}$.分析 a1,a3,a9构成等比数列{bn}的前3项,可得${a}_{3}^{2}$=a1a9,化为:a1=d.代入$\frac{{{a_1}+{a_3}+{a_6}}}{{{a_2}+{a_4}+{a_{10}}}}$,即可得出.
解答 解:∵a1,a3,a9构成等比数列{bn}的前3项,
∴${a}_{3}^{2}$=a1a9,
∴$({a}_{1}+2d)^{2}$=a1(a1+8d),
化为:a1=d.
∴$\frac{{{a_1}+{a_3}+{a_6}}}{{{a_2}+{a_4}+{a_{10}}}}$=$\frac{3{a}_{1}+7d}{3{a}_{1}+13d}$=$\frac{10d}{16d}$=$\frac{5}{8}$.
故答案为:$\frac{5}{8}$.
点评 本题考查了等差数列与等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.已知p:函数f(x)=$\frac{{\sqrt{4-{x^2}}}}{x+4}$-m有零点,q:|m|≤$\frac{{\sqrt{3}}}{3}$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
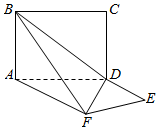 平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.
平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.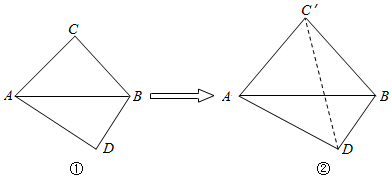
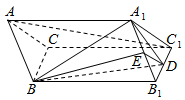 如图,在三棱柱ABC-A1B1C1中,A1B1=A1C1,点D,E分别是B1C1,A1B1的中点,AA1=AB=BD=1,∠A1AB=60°.
如图,在三棱柱ABC-A1B1C1中,A1B1=A1C1,点D,E分别是B1C1,A1B1的中点,AA1=AB=BD=1,∠A1AB=60°.