题目内容
19.方程|x2-a|-x+2=0(a>0)有两个不等的实数根,则实数a的取值范围是a>4.分析 题意转化为函数y=|x2-a|(a>0)与函数y=x-2的图象有两个交点,从而结合图象求解.
解答 解:∵方程|x2-a|-x+2=0(a>0)有两个不等的实数根,
∴函数y=|x2-a|(a>0)与函数y=x-2的图象有两个交点,
作函数y=|x2-a|(a>0)与函数y=x-2的图象如下, ,
,
结合图象可得,
存在x>2时,x2-a=0,
故a>4;
故答案为:a>4.
点评 本题考查了方程的根与函数的图象的交点的关系应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在等差数列{an}中,Sn为其前n项和,S7=35,a2+a3+a10=12,则Sn的最大值为( )
| A. | 28 | B. | 36 | C. | 45 | D. | 55 |
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AB,点M、N分别是线段A1C1,A1B的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AB,点M、N分别是线段A1C1,A1B的中点.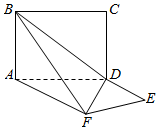 平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.
平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.