题目内容
3.若$cos(\frac{π}{2}-α)=\frac{{\sqrt{2}}}{3}$,则cos(π-2α)=$-\frac{5}{9}$.分析 由已知利用诱导公式,二倍角的余弦函数公式即可计算得解.
解答 解:∵$cos(\frac{π}{2}-α)=\frac{{\sqrt{2}}}{3}$,
∴sinα=$\frac{\sqrt{2}}{3}$,
∴cos(π-2α)=-cos2α=-(1-2sin2α)=2×($\frac{\sqrt{2}}{3}$)2-1=$-\frac{5}{9}$.
故答案为:$-\frac{5}{9}$.
点评 本题主要考查了诱导公式,二倍角的余弦函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如果二次方程x2-px-q=0(其中p,q均是大于0的整数)的正根小于3,那么这样的二次方程有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
15.已知a=log23,b=${log_{\frac{1}{2}}}3$,c=3${\;}^{\frac{1}{2}}$,则( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | a>c>b |
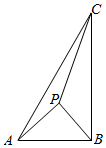 如图,在△ABC中,∠ABC=90°,AB=1,BC=$\sqrt{3}$,P为△ABC内一点,∠APB=90°.
如图,在△ABC中,∠ABC=90°,AB=1,BC=$\sqrt{3}$,P为△ABC内一点,∠APB=90°.