题目内容
1．在△ABC中，a，b，c分别为角A，B，C的对边，满足sinB（sinB+sinA）+（cosC-cosA）（cosC+cosA）=0，S△ABC=4$\sqrt{3}$，则ab=16．分析 对条件进行化简，结合正弦定理得出三边a，b，c的关系，利用余弦定理求出C．代入面积公式得出ab．
解答 解：∵sinB（sinB+sinA）+（cosC-cosA）（cosC+cosA）=0，
∴sin2B+sinAsinB+cos2C-cos2A=0，∴sin2B+sinAsinB+1-sin2C-（1-sin2A）=0，∴sin2A+sin2B-sin2C+sinAsinB=0．
∴a2+b2-c2=-ab，∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$．∴sinC=$\frac{\sqrt{3}}{2}$．
∵S△ABC=$\frac{1}{2}absinC$=4$\sqrt{3}$，∴ab=16．
故答案为16．
点评 本题考查了三角函数的恒等变换，及利用正余弦定理解三角形．属于中档题．
练习册系列答案
学业测评一课一测系列答案
相关题目
12．如表示采集的商品零售额（万元）与商品流通费率的一组数据：
（1）将商品零售额作为横坐标，商品流通费率作为纵坐标，在平面直角坐标系内作出散点图；
（2）商品零售额与商品流通费率具有线性相关关系吗？如果商品零售额是20万元，那么能否预测此时流通费率是多少呢？（b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$ a=$\overline{y}$-b$\overline{x}$）
| 商品零售额 | 9.5 | 11.5 | 13.5 | 15.5 | 17.5 | 19.5 | 21.5 | 23.5 | 25.5 | 27.5 |
| 商品流通费率 | 6.0 | 4.6 | 4.0 | 3.2 | 2.8 | 2.5 | 2.4 | 2.3 | 2.2 | 2.1 |
（2）商品零售额与商品流通费率具有线性相关关系吗？如果商品零售额是20万元，那么能否预测此时流通费率是多少呢？（b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$ a=$\overline{y}$-b$\overline{x}$）
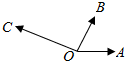如图所示，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，|$\overrightarrow{OC}$|=$\sqrt{3}$，∠AOB=60°，$\overrightarrow{OB}$⊥$\overrightarrow{OC}$．若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，则x，y的值分别是（ ）
10．有一个正三角形的两个顶点在抛物线y2=2px（p＞0）上，另一顶点在原点，则该三角形的边长是（ ）
| A． | 2$\sqrt{3}$p | B． | 4$\sqrt{3}$p | C． | 6$\sqrt{3}$p | D． | 8$\sqrt{3}$p |