题目内容
7.已知函数f(x)=lnx,g(x)=x-$\frac{1}{2}$x2.(Ⅰ)若点P是函数f(x)=lnx上任意一点,求点P到直线y=x+1的最小距离;
(Ⅱ)当x>e时,求证函数f(x)=lnx的图象位g(x)=x-$\frac{1}{2}$x2图象的上方.
分析 (Ⅰ)设x-y+m=0与函数f(x)=nx的图象相切于点P(x0,y0).求导,解得x0.再利用点到直线的距离公式即可得出.
(II)构造新函数h(x)=f(x)-g(x),求出h(x)的导函数,判断出h′(x)>0在(1,+∞)上恒成立,判断出h(x)递增,求出h(x)的最小值,判断出最小值大于0,判断出h(x)>0,判断出f(x)>g(x),得证.
解答 解:(Ⅰ)设x-y+m=0与函数f(x)=lnx的图象相切于点P(x0,y0).
∴f′(x)=$\frac{1}{x}$=,
∴f′(x0)=$\frac{1}{{x}_{0}}$=1,
∵x0>0,
解得x0=1.
∴y0=1,
∴点P(1,1)到直线y=x+1的距离为最小距离d=$\frac{|1-1+1|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
(Ⅱ)设h(x)=f(x)-g(x)=lnx-x+$\frac{1}{2}$x2,x>e,
∴h′(x)=$\frac{1}{x}$-1+x=$\frac{{x}^{2}-x+1}{x}$>0恒成立,
∴h(x)在(e,+∞)为增函数,
∴h(x)>h(e)=lne-e+$\frac{1}{2}$e2=1-e+$\frac{1}{2}$e2=1+e($\frac{1}{2}$e-1)>0,
∴x>e时,函数f(x)=lnx的图象位g(x)=x-$\frac{1}{2}$x2图象的上方
点评 考查导数研究曲线上某点的切线方程以及点到直线的距离公式,利用了导数与斜率的关系,不等式常转化为求函数的最值,属于中档题

练习册系列答案
相关题目
12.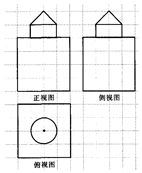 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )| A. | $({2\sqrt{2}+2})π+96$ | B. | $({2\sqrt{2}+1})π+96$ | C. | $({\sqrt{2}+2})π+96$ | D. | $({\sqrt{2}+1})π+96$ |
2.关于x的方程(m+3)x2-4mx+2m-1=0的两根异号,且负根的绝对值比正根大,那么实数m的取值范围为( )
| A. | (-3,0) | B. | (0,3) | C. | (-∞,-3)∪(0,+∞) | D. | (-∞,0)∪(3,+∞) |
19.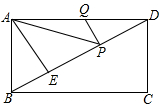 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
则AP+PQ的最小值为( )
 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,则AP+PQ的最小值为( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
17.设A={x|$\frac{1}{2}$<x<5,x∈Z},B={x|x≥a}.若A⊆B,则实数a的取值范围是( )
| A. | a<$\frac{1}{2}$ | B. | a≤$\frac{1}{2}$ | C. | a≤1 | D. | a<1 |