题目内容
12.过y2=4x的焦点F作两条弦AB和CD,且AB⊥x轴,|CD|=2|AB|,则弦CD所在直线的方程是x+y+1=0或x+y-1=0.分析 根据题意知AB为抛物线的通径进而求出|AB|和|CD|,满足条件的直线CD有两条,验证选项B,把直线和抛物线方程联立,求得x1+x2,进而根据抛物线的定义得出的|CD|符合题意.同样的方法可知x+y-1=0也符合题意.故可得出答案.
解答 解:依题意知AB为抛物线的通径,|AB|=2p=4,|CD|=2|AB|=8,
显然满足条件的直线CD有两条,
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=x-1}\end{array}\right.$得:x2-6x+1=0,x1+x2=6,此时|CD|=x1+x2+p=8,x+y+1=0符合题意.
同理,x+y-1=0也符合题意.
故答案是:x+y+1=0或x+y-1=0.
点评 本题主要考查了抛物线的性质,直线的一般式方程.属基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
20.若函数f(x)=$\left\{\begin{array}{l}\frac{a}{x},x>1\\(2-3a)x+1,x≤1\end{array}$是R上的减函数,则实数R的取值范围是 ( )
| A. | $(\frac{2}{3},1)$ | B. | $[\frac{3}{4},1)$ | C. | $(\frac{2}{3},\frac{3}{4}]$ | D. | ($\frac{2}{3}$,+∞) |
17.已知反比例函数y=$\frac{6}{x}$的图象与正比例函数y=$\frac{2}{3}$x的图象交于A,B两点,B点坐标为(-3,-2),则A点的坐标为( )
| A. | (-1,-6) | B. | (1,6) | C. | (3,2) | D. | (2,3) |
1.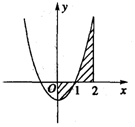 由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
 由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )| A. | ${∫}_{0}^{2}$(x 2-1)dx | B. | ${∫}_{0}^{2}$|(x 2-1)|dx | ||
| C. | |${∫}_{0}^{2}$(x 2-1)dx| | D. | ${∫}_{0}^{1}$(x 2-1)dx+${∫}_{1}^{2}$(x 2-1)dx |
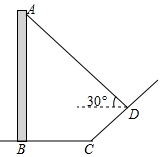 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号).
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号).