题目内容
16.已知函数f(x)=a(x-1)lnx+1(a∈R).(1)讨论函数f(x)的单调性;
(2)若x∈(1,+∞),f(x)>x-alnx恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;
(2)问题转化为axlnx+1-x>0在(1,+∞)恒成立,令g(x)=axlnx+1-x,(x>1),求出函数的导数,通过讨论a的范围判断函数的单调性,从而求出a的范围即可.
解答 解:(1)f′(x)=alnx+a-$\frac{a}{x}$,f″(x)=$\frac{a(x+1)}{{x}^{2}}$,
a>0时,f″(x)>0,f′(x)在(0,+∞)递增,
又f′(1)=0,∴x∈(0,1)时,f′(x)<0,f(x)递减,
x∈(1,+∞)时,f′(x)>0,f(x)递增;
a<0时,x∈(0,1)时,f′(x)>0,f(x)递增,
x∈(1,+∞)时,f′(x)<0,f(x)递减;
a=0时,f(x)=1,是常函数;
(2)若x∈(1,+∞),f(x)>x-alnx恒成立,
即axlnx+1-x>0在(1,+∞)恒成立,
令g(x)=axlnx+1-x,(x>1),
g′(x)=alnx+a-1,
a>0时,g′(x)递增,g′(1)=a-1,又g′(1)=0,
∴g′(a)≥0,即a-1≥0,解得:a≥1,
a≤0时,x→+∞时,g(x)→-∞不成立,
∴a≥1.
点评 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
1.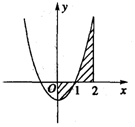 由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
 由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )| A. | ${∫}_{0}^{2}$(x 2-1)dx | B. | ${∫}_{0}^{2}$|(x 2-1)|dx | ||
| C. | |${∫}_{0}^{2}$(x 2-1)dx| | D. | ${∫}_{0}^{1}$(x 2-1)dx+${∫}_{1}^{2}$(x 2-1)dx |
5.f(x)是定义在R上图形关于y轴对称,且在[0,+∞)上是减函数,下列不等式一定成立的是( )
| A. | f[${\frac{2}{{2-{a^2}}}}$]<f(${{a^2}-2a+\frac{5}{4}}$) | B. | f[-cos60°]<f(tan30°) | ||
| C. | f[-(cos60°)2]≥f(${{a^2}-2a+\frac{5}{4}}$) | D. | f[-sin45°]>f(-3a+2) |
6.$\root{3}{-a}•\root{6}{a}$=( )
| A. | $-\sqrt{a}$ | B. | $-\sqrt{-a}$ | C. | $\sqrt{-a}$ | D. | $\sqrt{a}$ |
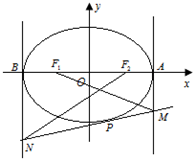 如图,已知椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上任意一点P(异于顶点)处的切线与该椭圆在长轴顶点A,B处的切线分别交于点M,N,该椭圆的左,右焦点分别是F1,F2,直线MF1,NF2的斜率分别是k1,k2.
如图,已知椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上任意一点P(异于顶点)处的切线与该椭圆在长轴顶点A,B处的切线分别交于点M,N,该椭圆的左,右焦点分别是F1,F2,直线MF1,NF2的斜率分别是k1,k2.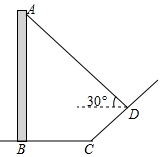 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号).
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号).