题目内容
设数列{an}满足a1=3,an+1=an2-2nan+2,n∈N*.
(Ⅰ)求出a2,a3,a4的值,并猜想数列{an}的通项公式(不需证明);
(Ⅱ)记Sn为数列{an}的前n项和,试求使得2n>Sn成立的最小正整数n,并给出证明.
(Ⅰ)求出a2,a3,a4的值,并猜想数列{an}的通项公式(不需证明);
(Ⅱ)记Sn为数列{an}的前n项和,试求使得2n>Sn成立的最小正整数n,并给出证明.
考点:数学归纳法
专题:等差数列与等比数列
分析:(Ⅰ)由a1=3,an+1=an2-2nan+2,n∈N*,可求得a2,a3,a4的值,并猜想数列{an}的通项公式;
(Ⅱ)Sn=
=n2+2n,使得2n>Sn成立的最小正整数n=6,利用数学归纳法证明即可.
(Ⅱ)Sn=
| n(3+2n+1) |
| 2 |
解答:
解 (Ⅰ)a2=5,a3=7,a4=9,猜想an=2n+1.…(4分)
(Ⅱ)Sn=
=n2+2n,…(6分)
使得2n>Sn成立的最小正整数n=6.…(7分)
下面给出证明:n≥6(n∈N*)时都有2n>n2+2n.
①n=6时,26>62+2×6,即64>48成立;…(8分)
②假设n=k(k≥6,k∈N*)时,2k>k2+2k成立,那么2k+1=2•2k>2(k2+2k)=k2+2k+k2+2k>k2+2k+3+2k=(k+1)2+2(k+1),即n=k+1时,不等式成立;
由①、②可得,对于所有的n≥6(n∈N*)
都有2n>n2+2n成立. …(12分)
(Ⅱ)Sn=
| n(3+2n+1) |
| 2 |
使得2n>Sn成立的最小正整数n=6.…(7分)
下面给出证明:n≥6(n∈N*)时都有2n>n2+2n.
①n=6时,26>62+2×6,即64>48成立;…(8分)
②假设n=k(k≥6,k∈N*)时,2k>k2+2k成立,那么2k+1=2•2k>2(k2+2k)=k2+2k+k2+2k>k2+2k+3+2k=(k+1)2+2(k+1),即n=k+1时,不等式成立;
由①、②可得,对于所有的n≥6(n∈N*)
都有2n>n2+2n成立. …(12分)
点评:本题考查递推数列与数学归纳法,考查运算、猜想及推理论证的能力,属于中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
已知集合A={x|x≤2},B={x|x(3-x)>0},则A∩B=( )
| A、{x|0<x≤2} |
| B、{x|x<0} |
| C、{x|x≤2,或x>3} |
| D、{x|x<0,或x≥2} |
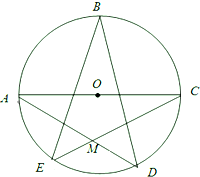 如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径.
如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径. 已知四边形ABCD是菱形,四边形BDEF是正方形,平面BDEF⊥平面ABCD,G、H、M分别是CE、CF、FB的中点.
已知四边形ABCD是菱形,四边形BDEF是正方形,平面BDEF⊥平面ABCD,G、H、M分别是CE、CF、FB的中点.