题目内容
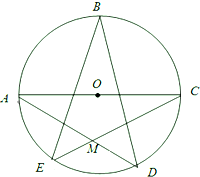 如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径.
如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径.(1)求∠A+∠B+∠C+∠D+∠E的值;
(2)若⊙O的半径为
| ||
| 2 |
考点:弦切角,与圆有关的比例线段
专题:直线与圆
分析:(Ⅰ)连接OA,OB,OC,OD,OE,圆心角和圆周角的关系求解.
(Ⅱ)连接OM和CD,∵AC为⊙O的直径,
∴∠ADC=90°,由已知条件推导出OA=
,AM=
=
=1.由此能求出MD的长.
(Ⅱ)连接OM和CD,∵AC为⊙O的直径,
∴∠ADC=90°,由已知条件推导出OA=
| ||
| 2 |
| OA |
| cosA |
| OA |
| cos30° |
解答:
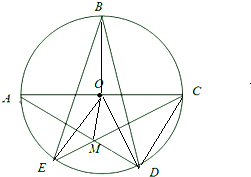 解:(Ⅰ)连接OA,OB,OC,OD,OE,
解:(Ⅰ)连接OA,OB,OC,OD,OE,
则∠A+∠B+∠C+∠D+∠E
=
(∠COD+∠DOE+∠EOA+∠AOB+∠BOC)
=
×360°=180°.(5分)
(Ⅱ)连接OM和CD,∵AC为⊙O的直径,
∴∠ADC=90°,又E、D为AC的三等分点,
∴∠A=∠C=
∠EOA=
×
×180°=30°.(7分)
∴OM⊥AC.∵⊙O的半径为
,即OA=
,
∴AM=
=
=1.
在Rt△ADC中,AD=AC•cosA=2×
×
=
.
则MD=AD-AM=
.(10分)
 解:(Ⅰ)连接OA,OB,OC,OD,OE,
解:(Ⅰ)连接OA,OB,OC,OD,OE,则∠A+∠B+∠C+∠D+∠E
=
| 1 |
| 2 |
=
| 1 |
| 2 |
(Ⅱ)连接OM和CD,∵AC为⊙O的直径,
∴∠ADC=90°,又E、D为AC的三等分点,
∴∠A=∠C=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
∴OM⊥AC.∵⊙O的半径为
| ||
| 2 |
| ||
| 2 |
∴AM=
| OA |
| cosA |
| OA |
| cos30° |
在Rt△ADC中,AD=AC•cosA=2×
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
则MD=AD-AM=
| 1 |
| 2 |
点评:本题考查五个角的和的求法,考查线段长的求法,解题时要认真审题,注意圆心角和圆周角的关系的合理运用.

练习册系列答案
相关题目
设m、n为两条不同直线,α、β为两个不同平面,则下列命题正确的是( )
| A、若m∥α,n∥β,m∥n,则α∥β |
| B、若m⊥α,n⊥β,m⊥n,则α⊥β |
| C、若α∥β,m?α,n?β,则m∥n |
| D、若α⊥β,α∩β=m,n⊥m,则n⊥β |
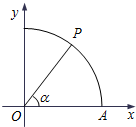 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.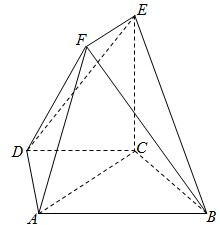 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=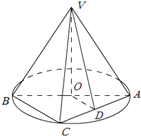 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.