题目内容
已知AD,CE分别是△ABC的边BC,AB的中线,且
=
,
=
,则
= (用
,
表示)
| AD |
| a |
| CE |
| b |
| AC |
| a |
| b |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,由AD,CE分别是△ABC的边BC,AB的中线,可得
=
(
+
),
=
(
+
),变形化化简即可得出.
| AD |
| 1 |
| 2 |
| AB |
| AC |
| CE |
| 1 |
| 2 |
| CA |
| CB |
解答:
解:如图所示,
∵AD,CE分别是△ABC的边BC,AB的中线,
∴
=
(
+
),
=
(
+
),
∴
+
=2
=2
,
-
+(
-
)=2
=2
,
∴3
=2
-2
,
∴
=
(
-
).
故答案为:
(
-
).

∵AD,CE分别是△ABC的边BC,AB的中线,
∴
| AD |
| 1 |
| 2 |
| AB |
| AC |
| CE |
| 1 |
| 2 |
| CA |
| CB |
∴
. |
| AC |
| AB |
| AD |
| a |
-
| AC |
| AB |
| AC |
| CE |
| b |
∴3
| AC |
| a |
| b |
∴
| AC |
| 2 |
| 3 |
| a |
| b |
故答案为:
| 2 |
| 3 |
| a |
| b |
点评:本题考查了的平行四边形与三角形法则、线性运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
给定△ABC,若点D满足
=
,
=
+λ
,则λ等于( )
| AD |
| 2 |
| 3 |
| AB |
| CD |
| 1 |
| 3 |
| CA |
| CB |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
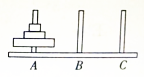 从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.
从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.