题目内容
4.已知向量$\overrightarrow a,\overrightarrow b$的夹角为120°,且$|\overrightarrow a|=1$,$|\overrightarrow b|=2$,则向量$\overrightarrow a+\overrightarrow b$在向量$\overrightarrow a$方向上的投影是( )| A. | 0 | B. | $\frac{2}{3}$ | C. | -1 | D. | $\frac{1}{2}$ |
分析 根据平面向量数量积与投影的定义,计算即可.
解答 解:向量$\overrightarrow a,\overrightarrow b$的夹角为θ=120°,
且$|\overrightarrow a|=1$,$|\overrightarrow b|=2$,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$=${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$•$\overrightarrow{b}$=12+1×2×cos120°=0;
∴向量$\overrightarrow a+\overrightarrow b$在向量$\overrightarrow a$方向上的投影是
|$\overrightarrow{a}$+$\overrightarrow{b}$|cos<$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{a}$>=|$\overrightarrow{a}$+$\overrightarrow{b}$|×$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}+\overrightarrow{b}|×|\overrightarrow{a}|}$=$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}|}$=0.
故选:A.
点评 本题考查了平面向量数量积与投影的定义和应用问题,是基础题.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 18 | B. | 24 | C. | 30 | D. | 60 |
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
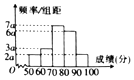 已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.
已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.