题目内容
已知函数f(x)=
的定义域是 ．
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件即可求函数的定义域．
解答：
解：要使函数有意义，则
≥0，
即（x+1）（x-2）≥0且x-2≠0，
即x＞2或x≤-1，
即函数的定义域为：（-∞，-1]∪（2，+∞），
故答案为：（-∞，-1]∪（2，+∞）
| x+1 |
| x-2 |
即（x+1）（x-2）≥0且x-2≠0，
即x＞2或x≤-1，
即函数的定义域为：（-∞，-1]∪（2，+∞），
故答案为：（-∞，-1]∪（2，+∞）
点评：本题主要考查函数定义域的求法，要求熟练掌握常见函数成立的条件，比较基础．
练习册系列答案
相关题目
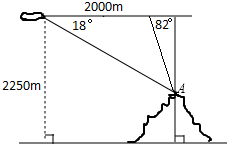如图，一只气球在2250m的高空水平飞行，气球上的工作人员测得前方一座山顶上A点处的俯角为18°，当气球向前飞行了2000m后，又测得前方A点处的俯角为82°，则山的高度为已知y=f（x）是定义域为R的奇函数，且当x＞0时，f（x）=2x+x3-4．若存在x0∈I，使得f（x0）=0，则区间I不可能是（ ）
| A、（-2，-1） |
| B、（-1，1） |
| C、（1，2） |
| D、（-1，0） |