题目内容
已知m、n、l是三条不同的直线,α、β、γ是三个不同的平面,给出以下命题:
①若m?α,n∥α,则m∥n;
②若m?α,n?β,α⊥β,α∩β=l,m⊥l,则m⊥n;
③若n∥m,m?α,则n∥α;
④若α∥γ,β∥γ,则α∥β.
其中正确命题的序号是 .
①若m?α,n∥α,则m∥n;
②若m?α,n?β,α⊥β,α∩β=l,m⊥l,则m⊥n;
③若n∥m,m?α,则n∥α;
④若α∥γ,β∥γ,则α∥β.
其中正确命题的序号是
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①利用线面平行的性质即可得出;
②利用面面垂直的性质定理即可得出;
③利用线面平行的判定定理即可得出;
④利用面面平行的传递性即可得出.
②利用面面垂直的性质定理即可得出;
③利用线面平行的判定定理即可得出;
④利用面面平行的传递性即可得出.
解答:
解:①若m?α,n∥α,利用线面平行的性质可得m∥n或为异面直线,因此不正确;
②若m?α,n?β,α⊥β,α∩β=l,m⊥l,利用面面垂直的性质定理可得m⊥n,正确;
③若n∥m,m?α,则n∥α或n?α,因此不正确;
④若α∥γ,β∥γ,利用面面平行的传递性可得:α∥β,正确.
综上可知:只有②④正确.
故答案为:②④.
②若m?α,n?β,α⊥β,α∩β=l,m⊥l,利用面面垂直的性质定理可得m⊥n,正确;
③若n∥m,m?α,则n∥α或n?α,因此不正确;
④若α∥γ,β∥γ,利用面面平行的传递性可得:α∥β,正确.
综上可知:只有②④正确.
故答案为:②④.
点评:本题综合考查了空间线面面面位置关系,属于基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
已知a,b∈R且a≠b,若aea=beb(e为自然对数的底数),则下列正确的是( )
| A、lna-lnb=b-a |
| B、lna-lnb=a-b |
| C、ln(-a)-ln(-b)=b-a |
| D、ln(-a)-ln(-b)=a-b |
执行如图所示的程序框图,则输出S的值为( )
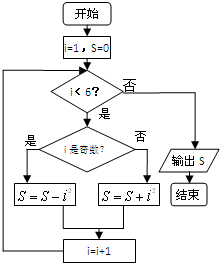

| A、3 | B、-6 | C、10 | D、-15 |
 正四面体ABCD边长为2.E,F分别为AC,BD中点.
正四面体ABCD边长为2.E,F分别为AC,BD中点.