题目内容
5.已知sinα=3cosα,则$\frac{sin2α}{1+cos2α}$=3.分析 由条件求得tanα=3,再利用同角三角函数的基本关系、二倍角公式求得$\frac{sin2α}{1+cos2α}$的值.
解答 解:sinα=3cosα,∴tanα=3,则$\frac{sin2α}{1+cos2α}$=$\frac{2sinαcosα}{{2cos}^{2}α}$=tanα=3,
故答案为:3.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.若a=2x,b=$\sqrt{x}$,c=log${\;}_{\frac{1}{2}}$x,则“x>1”是“a>b>c”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
13.已知函数f(x)=x2-2x+1+alnx有两个极值点x1,x2,且x1<x2,则实数a的取值范围为( )
| A. | $({-∞,\frac{1}{2}})$ | B. | $({0,\frac{1}{2}})$ | C. | $({\frac{1}{2},+∞})$ | D. | $({0,\frac{1}{2}}]$ |
10.函数f(x)=sinx-2cosx=$\sqrt{5}$sin(x+φ),则cosφ等于( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
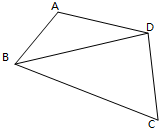 如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值.
如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值. 如图,在正方体ABCD-A1B1C1D1中,E为棱CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,E为棱CC1的中点. 设函数f(x)=Asin(ωx+φ),(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(100)=2+2$\sqrt{2}$.
设函数f(x)=Asin(ωx+φ),(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(100)=2+2$\sqrt{2}$.