题目内容
4.设A-B={x|x∈A,x∉B},若M={x|x=$\sqrt{2}$(sinα+cosα)},N={x|x=sinα-|sinα|},则M-N={x|0<x≤2}.分析 求出集合M,集合N.利用定义求解即可.
解答 解:M={x|x=$\sqrt{2}$(sinα+cosα)}={x|x=2sin(α+$\frac{π}{4}$)}={x|-2≤x≤2}
N={x|x=sinα-|sinα|}={x|-2≤x≤0},
M-N={x|0<x≤2}.
故答案为:{x|0<x≤2}.
点评 本题考查集合的基本运算,考查计算能力.

练习册系列答案
相关题目
16.若a=2x,b=$\sqrt{x}$,c=log${\;}_{\frac{1}{2}}$x,则“x>1”是“a>b>c”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
13.已知函数f(x)=x2-2x+1+alnx有两个极值点x1,x2,且x1<x2,则实数a的取值范围为( )
| A. | $({-∞,\frac{1}{2}})$ | B. | $({0,\frac{1}{2}})$ | C. | $({\frac{1}{2},+∞})$ | D. | $({0,\frac{1}{2}}]$ |
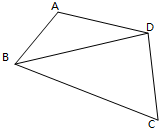 如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值.
如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值. 设函数f(x)=Asin(ωx+φ),(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(100)=2+2$\sqrt{2}$.
设函数f(x)=Asin(ωx+φ),(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(100)=2+2$\sqrt{2}$.