题目内容
4.已知函数f(x)=m•2x+2•3x,m∈R.(1)当m=-9时,求满足f(x+1)>f(x)的实数x的范围;
(2)若$f(x)≤{(\frac{9}{2})^x}$对任意的x∈R恒成立,求实数m的范围.
分析 (1)由题意可得2•3x+1-9•2x+1+>2•3x-9•2x,化简可得,2x-2<3x-2,即为($\frac{3}{2}$)x-2>1=($\frac{3}{2}$)0,再由指数函数的单调性,解不等式即可得到所求范围;
(2)由题意可得$m≤{(\frac{3}{2})^{2x}}-2{(\frac{3}{2})^x}$,令$t={(\frac{3}{2})^x}>0$,即有m≤t2-2t的最小值,运用配方可得最小值,即可得到所求范围.
解答 解:(1)当m=-9时,f(x)=-9•2x+2•3x,
f(x+1)>f(x),即为2•3x+1-9•2x+1>2•3x-9•2x,
化简可得,2x-2<3x-2,即为($\frac{3}{2}$)x-2>1=($\frac{3}{2}$)0,
即有x-2>0,
解得,x>2;
(2)由$f(x)≤{(\frac{9}{2})^x}$恒成立,即为m•2x+2•3x≤($\frac{9}{2}$)x,
可得$m≤{(\frac{3}{2})^{2x}}-2{(\frac{3}{2})^x}$,
令$t={(\frac{3}{2})^x}>0$,
即有m≤t2-2t的最小值,
由(t2-2t)min=-1,
可得m≤-1,即实数m的范围是(-∞,-1].
点评 本题考查指数不等式的解法,注意运用指数函数的单调性和运算性质,考查不等式恒成立问题的解法,注意运用分离参数和换元法,以及二次函数的最值的求法,属于中档题.

练习册系列答案
相关题目
15.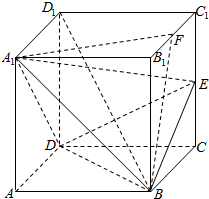 已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.
(1)求证;BD⊥A1E;
(2)求证:平面A1BD⊥平面EBD;
(3)求证:平面A1BF⊥平面A1BD.
 已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.(1)求证;BD⊥A1E;
(2)求证:平面A1BD⊥平面EBD;
(3)求证:平面A1BF⊥平面A1BD.
12.函数$f(x)=\frac{{{e^{2x}}-1}}{e^x}$的图象关于( )
| A. | 原点对称 | B. | y轴对称 | C. | x轴对称 | D. | 关于x=1对称 |
13.$\int_0^1{3{x^2}dx-\int_0^1{\sqrt{1-{x^2}}dx=}}$( )
| A. | $1-\frac{π}{4}$ | B. | 2 | C. | $1+\frac{π}{4}$ | D. | π-1 |
