题目内容
15.若数列{an}满足a1=2,an+1=an+log2(1-$\frac{1}{n+1}$),则a32=-3.分析 根据累加法和对数的运算性质即可求出数列的通项公式,代值计算即可.
解答 解:∵an+1=an+log2(1-$\frac{1}{n+1}$)=log2($\frac{n}{n+1}$),
∴an+1-an=log2($\frac{n}{n+1}$)
∴a2-a1=log2$\frac{1}{2}$,
a3-a2=log2$\frac{2}{3}$,
…
an-an-1=log2$\frac{n-1}{n}$
∴(a2-a1)+(a3-a2)+…+(an-an-1)=log2($\frac{1}{2}$×$\frac{2}{3}$…×$\frac{n-1}{n}$)=log2($\frac{1}{2n}$)=-log2n
∴an-2=-log2n,
∴an=2-log2n,
∴a32=2-log232=-3,
故答案为:-3.
点评 本题考查数列的通项,涉及对数的简单性质,注意解题方法的积累,属于中档题

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
5.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2$\sqrt{3}$,则|$\overrightarrow{a}$|=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | 3 |
3.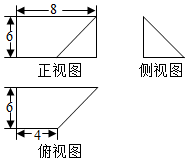 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )| A. | 72 | B. | 80 | C. | 120 | D. | 144 |
7.下列函数中,既是偶函数又在区间(1,2)内单调递减的是( )
| A. | f(x)=-cosx | B. | f(x)=2x+2-x | C. | f(x)=$\frac{1}{{x}^{2}}$ | D. | f(x)=$\sqrt{-x}$ |
