题目内容
13．如果方程x2-4ax+3a2=0的一根小于1，另一根大于1，那么实数a的取值范围是（ ）| A． | $\frac{1}{3}＜a＜1$ | B． | a＞1 | C． | $a＜\frac{1}{3}$ | D． | a=1 |
分析 利用一元二次方程的根的分布与系数的关系，二次函数的性质，求得a的取值范围．
解答 解：∵方程x2-4ax+3a2=0的一根小于1，另一根大于1，
令f（x）=x2-4ax+3a2，函数的开口向上，
则f（1）=1-4a+3a2＜0，求得$\frac{1}{3}$＜a＜1，
故选：A．
点评 本题主要考查一元二次方程的根的分布与系数的关系，二次函数的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
6．已知f（sinx）=cos2x-1，则f（cos15°）=（ ）
| A． | $-\frac{1}{2}$ | B． | $-\frac{3}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}-1$ | D． | $\frac{{\sqrt{3}}}{2}-1$ |
4．若将函数y=sin（2x+φ）（0＜φ＜π）图象向右平移$\frac{π}{8}$个单位长度后关于y轴对称，则φ的值为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{3π}{8}$ | C． | $\frac{3π}{4}$ | D． | $\frac{5π}{8}$ |
8．如果一个函数f（x）满足：（1）定义域为R；（2）任意x1，x2∈R，若x1+x2=0，则f（x1）+f（x2）=0；（3）任意x∈R，若t＞0，总有f（x+t）＞f（x），则f（x）可以是（ ）
| A． | y=-x | B． | y=3x | C． | y=x3 | D． | y=log3x |
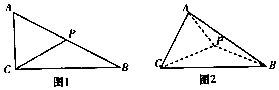如图1，在△ABC中，AC=2，∠ACB=90°，∠ABC=30°，P是AB边的中点，现把△ACP沿CP折成如图2所示的三棱锥A-BCP，使得$AB=\sqrt{10}$．