题目内容
已知f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,设a=f(log47),b=f(log23),c=f(0.20.6),则a,b,c的大小关系是( )
| A、c<b<a |
| B、b<c<a |
| C、b<a<c |
| D、a<b<c |
考点:奇偶性与单调性的综合,对数值大小的比较
专题:综合题,函数的性质及应用
分析:由f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,可得出自变量的绝对值越小,函数值越大,由此问题转化为比较自变量的大小,问题即可解决.
解答:
解:f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,要得函数在(0,+∞)上是减函数,
图象越靠近y轴,图象越靠上,即自变量的绝对值越小,函数值越大,
由于0<0.20.6<1<log47<log49=log23,
可得b<a<c,
故选C.
图象越靠近y轴,图象越靠上,即自变量的绝对值越小,函数值越大,
由于0<0.20.6<1<log47<log49=log23,
可得b<a<c,
故选C.
点评:本题解答的关键是根据函数的性质得出自变量的绝对值越小,函数值越大这一特征,由此转化为比较自变量的大小,使得问题容易解决.这也是本题解答的亮点.

练习册系列答案
相关题目
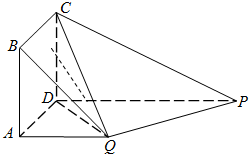 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=| 1 |
| 2 |
(1)求证:PQ⊥平面DCQ;
(2)若AQ=2,求四面体C-BDQ的体积.
若U={1,2,3,4,5,6,7},A={3,4,6,7},B={3,5,6,7},则∁U(A∩B)=( )
| A、{1,2,4,5} |
| B、{2,6,8} |
| C、{1,3,5,7} |
| D、{1,2} |
若M⊆U,N⊆U,且M⊆N,则( )
| A、M∩N=N |
| B、M∪N=M |
| C、∁UN⊆∁UM |
| D、∁UM⊆∁UN |
“cos2α=-
”是“cosα=
”的( )
| 7 |
| 25 |
| 4 |
| 5 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |