题目内容
1.给出下列命题:①将函数y=cos(x+$\frac{3π}{2}$)的图象上的每个点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),再向左平移$\frac{π}{4}$个单位长度,得到函数y=sin(2x+$\frac{π}{4}$)的图象;
②设随机变量ξ-N(3,9),若P(ξ<a)=0.3(a<3)则P(ξ<6-a)=0.7
③(2$\sqrt{x}$-$\frac{1}{x}$)10的二项展开式中含有x-1项的二项式系数是210;
④已知数列{an}为等差数列,且a2013+a2015=${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx,则a2014•(a2012+2a2014+a2016)的值为4π2.
其中正确的命题的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①根据三角函数的图象关系进行判断.
②根据正态分布的性质进行判断,
③根据二项展开式的公式进行判断.
④根据等差数列的性质以及积分的应用进行求解判断.
解答 解:①函数y=cos(x+$\frac{3π}{2}$)=cos(x+2π-$\frac{π}{2}$)=sinx,将图象上的每个点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),得到y=sin2x,
再向左平移$\frac{π}{4}$个单位长度,得到函数y=sin2(x+$\frac{π}{4}$)的图象;故①错误,
②设随机变量ξ-N(3,9),若P(ξ<a)=0.3(a<3),则P(ξ<a)=P(ξ>6-a),则P(ξ<6-a)=1-P(ξ>6-a)=1-0.3=0.7,故②正确,
③(2$\sqrt{x}$-$\frac{1}{x}$)10的二项展开式中的通项公式Tk+1=C${\;}_{10}^{k}$(2$\sqrt{x}$)10-k(-$\frac{1}{x}$)k=C${\;}_{10}^{k}$(2$\sqrt{x}$)10-k(-$\frac{1}{x}$)k=C${\;}_{10}^{k}$•210-k(-1)kx${\;}^{5-\frac{3k}{2}}$,
当5-$\frac{3k}{2}$=-1时,k=4,此时T5=C${\;}_{10}^{4}$26x-1=210×64x-1=13440x-1
故x-1项的二项式系数是13440,故③错误;
④已知数列{an}为等差数列,且a2013+a2015=${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx=$\frac{1}{2}×π×{2}^{2}$=2π,即a2014=π,
则a2014•(a2012+2a2014+a2016)=a2014×4a2014=4π2.故④正确,
故正确的是②④,
故选:C
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 20 | 40 |
(1)某公司一次性从4S店购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年内需要维修的车辆数,求ξ的分布列及数学期望(各型汽车维修的频率视为其需要维修的概率);
(2)该品牌汽车4S店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.
| 单价x(元) | 800 | 820 | 840 | 850 | 880 | 900 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
预计在今后的销售中,销量与单价仍然服从$\widehat{y}$=bx+a(b=0.2,a=$\widehat{y}$-b$\widehat{x}$)的关系,且该产品的成本是500元/件,为使4S店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元.
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 锐角或钝角三角形 |
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
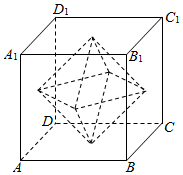 如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求:
如图所示,用一棱长为a的正方体,制作一以各面中心为顶点的正八面体.求: