题目内容
13．
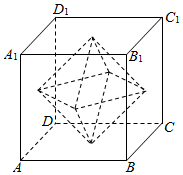如图所示，用一棱长为a的正方体，制作一以各面中心为顶点的正八面体．求：（1）此正八面体的表面积S；
（2）此正八面体的体积V．
分析 （1）求出八面体的棱长，然后求解表面积即可．
（2）八面体分成两个正四棱锥，两个底面面积，然后求出体积即可．
解答 解：（1）正方体的棱长为a，将正方体的六个面的中心连接起来，构成一个八面体，八面体的棱长为：$\frac{\sqrt{2}}{2}a$，八面体的表面积为：8×$\frac{\sqrt{3}}{4}×（\frac{\sqrt{2}a}{2}）^{2}$=$\sqrt{3}$a2．
（2）八面体分成两个正四棱锥，底面面积为：$\frac{1}{2}$a2，高为$\frac{1}{2}$a，一个正四棱锥的体积为：$\frac{1}{3}$×$\frac{1}{2}$a2×$\frac{1}{2}$a
所以这个八面体的体积是：2×$\frac{1}{3}$×$\frac{1}{2}$a2×$\frac{1}{2}$a=$\frac{1}{6}$a3．
点评 本题考查棱锥的体积和表面积的求法，正方体的内接体的知识，解题关键在八面体转化为两个正四棱锥，是常考题型．
练习册系列答案
相关题目
3．设θ为第四象限的角，cosθ=$\frac{4}{5}$，则sin2θ=（ ）
| A． | $\frac{7}{25}$ | B． | $\frac{24}{25}$ | C． | -$\frac{7}{25}$ | D． | -$\frac{24}{25}$ |
10．若数列{an}中，满足：a1=1，a2=3，且2nan=（n-1）an-1+（n+1）an+1，则a10的值是（ ）
| A． | 4$\frac{1}{5}$ | B． | 4$\frac{2}{5}$ | C． | 4$\frac{3}{5}$ | D． | 4$\frac{4}{5}$ |
如图，三棱锥S-ABC，E、F分别在线段AB、AC上，EF∥BC，△ABC、△SEF均是等边三角形，且平面SEF⊥平面ABC，若BC=4，EF=a，O为EF的中点．
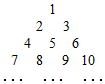已知数阵：