题目内容
10.若椭圆上存在三点,使得这三点与椭圆中心恰好是一个正方形的四个顶点,则该椭圆的离心率为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 由正方形和椭圆的对称性可得,设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由B(a,0),OABC为正方形,可得A($\frac{a}{2}$,$\frac{a}{2}$),C($\frac{a}{2}$,-$\frac{a}{2}$),代入椭圆方程,可得a2=3b2,由a,b,c的关系,结合离心率公式,可得所求值.
解答 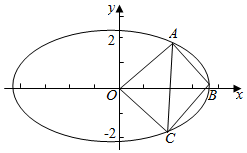 解:由正方形和椭圆的对称性可得,
解:由正方形和椭圆的对称性可得,
设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由B(a,0),OABC为正方形,可得
A($\frac{a}{2}$,$\frac{a}{2}$),C($\frac{a}{2}$,-$\frac{a}{2}$),
将A的坐标代入椭圆方程可得
$\frac{{a}^{2}}{4{a}^{2}}$+$\frac{{a}^{2}}{4{b}^{2}}$=1,
即有a2=3b2,
c2=a2-b2=$\frac{2}{3}$a2,
即有e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$.
故选:D.
点评 本题考查椭圆的离心率的求法,注意运用椭圆的性质:对称性,考查点满足椭圆方程,以及计算能力,属于中档题.

练习册系列答案
相关题目
18.点(0,-1)到直线3x-4y+6=0的距离是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{9}{5}$ | D. | 2 |
15.△ABC中,角A,B,C所对的边分别为a,b,c,若$\frac{a}{sinB}=\frac{b}{sinC}=\frac{c}{sinA}$,三角形ABC的形状是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
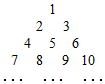 已知数阵:
已知数阵: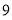 ,当其外接球的体积最小时, 它的高为( )
,当其外接球的体积最小时, 它的高为( )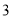 B.
B.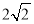 C.
C.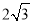 D.
D.