题目内容
9.设f(x)=-3sin(2x+φ)(-π<φ<π),若f(x)≤f($\frac{π}{6}$)恒成立,则φ=$\frac{π}{6}$.分析 由题意可得 2x+φ=2kπ-$\frac{π}{2}$,存在k∈Z,使kπ-$\frac{π}{4}$-φ=$\frac{π}{6}$,由此求得φ的值.
解答 解:由题意可得f($\frac{π}{6}$)为函数f(x)的最大值为3,即 2x+φ=2kπ-$\frac{π}{2}$,
求得x=kπ-$\frac{π}{4}$-φ,故存在k∈Z,使kπ-$\frac{π}{4}$-φ=$\frac{π}{6}$,故φ=$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题主要考查正弦函数的图象,正弦函数的最值,属于基础题.

练习册系列答案
相关题目
4.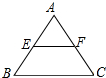 在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
 在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |