题目内容
设数列{an}：1，－2，－2，3，3，3，－4，－4，－4，－4，…，(－1)k－1k，…，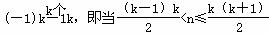 
(k∈N*)时，an＝(－1)k－1k，记Sn＝a1＋a2＋…＋an(n∈N*)，用数学归纳法证明Si(2i＋1)＝－i(2i＋1)(i∈N*)．
证明：①当i＝1时，Si(2i＋1)＝S3＝－1·(2＋1)＝－3，
故原式成立．
②假设当i＝m时，等式成立，即Sm(2m＋1)＝－m·(2m＋1)．
则当i＝m＋1时，
S(m＋1)[2(m＋1)＋1]＝S(m＋1)(2m＋3)＝Sm(2m＋1)＋(2m＋1)2－(2m＋2)2＝－m(2m＋1)＋(2m＋1)2－(2m＋2)2 ＝－(2m2＋5m＋3)＝－(m＋1)(2m＋3)，故原式成立．
综合①②得：Si(2i＋1)＝－i(2i＋1)．
练习册系列答案
相关题目
的部分图象为（ ） 
A B 
的展开式中含
的项的系数是 （用数字作答）．