题目内容
已知双曲线过点(3，－2)，且与椭圆4x2＋9y2＝36有相同的焦点．
(1) 求双曲线的标准方程；
(2) 求以双曲线的右准线为准线的抛物线的标准方程．
解：(1) 由题意，椭圆4x2＋9y2＝36的焦点为(±
，0)，即c＝，
∴ 设所求双曲线的方程为
＝1，
∵ 双曲线过点(3，－2)，
∴
＝1, ∴ a2＝3或a2＝15(舍去)．
故所求双曲线的方程为
＝1.
(2) 由(1)可知双曲线的右准线为 x＝
.
设所求抛物线的标准方程为y2＝－2px(p>0)，则p＝
，故所求抛物线的标准方程为y2＝－
x.
练习册系列答案
阅读快车系列答案
相关题目
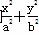＝1(a＞b＞0)的两个焦点，P为椭圆C上一点，且
.若△PF1F2的面积为9，则b＝________. 
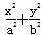＝1(a>b>0)经过点M(－2，－1)，离心率为
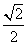.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
＝1的两个焦点，P是双曲线上的一点，且3PF1＝4PF2，则△PF1F2的面积等于________．
＝1的右焦点为(3，0)，则该双曲线的离心率为________．
x是指数函数(小前提)，所以y＝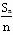
为等差数列，公差为
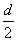.类似地，若各项均为正数的等比数列{bn}的公比为q，前n项的积为Tn，则数列{
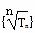}为等比数列，公比为________．
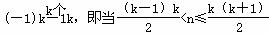(k∈N*)时，an＝(－1)k－1k，记Sn＝a1＋a2＋…＋an(n∈N*)，用数学归纳法证明Si(2i＋1)＝－i(2i＋1)(i∈N*)．