题目内容
用数学归纳法证明an+1+(a+1)2n-1能被a2+a+1整除(n∈N*).
证明:① 当n=1时,a2+(a+1)=a2+a+1可被a2+a+1整除.
② 假设n=k(k∈N*)时,ak+1+(a+1)2k-1能被a2+a+1整除,则当n=k+1时,ak+2+(a+1)2k+1=a·ak+1+(a+1)2(a+1)2k-1=a·ak+1+a·(a+1)2k-1+(a2+a+1)(a+1)2k-1=a[ak+1+(a+1)2k-1]+(a2+a+1)(a+1)2k-1,由假设可知a[ak+1+(a+1)2k-1]能被a2+a+1整除,(a2+a+1)(a+1)2k-1也能被a2+a+1整除,∴ ak+2+(a+1)2k+1能被a2+a+1整除,即n=k+1时命题也成立,
∴ 对任意n∈N*原命题成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
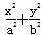 =1(a>b>0)经过点M(-2,-1),离心率为
=1(a>b>0)经过点M(-2,-1),离心率为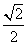 .过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.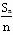 为等差数列,公差为
为等差数列,公差为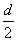 .类似地,若各项均为正数的等比数列{bn}的公比为q,前n项的积为Tn,则数列{
.类似地,若各项均为正数的等比数列{bn}的公比为q,前n项的积为Tn,则数列{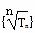 }为等比数列,公比为________.
}为等比数列,公比为________.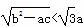
 +
+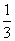 +…+
+…+ <n,其中n>1且n∈N*,在验证n=2时,式子的左边等于________.
<n,其中n>1且n∈N*,在验证n=2时,式子的左边等于________.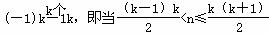 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*). 等于
等于 (B)
(B) (C)
(C) (D)
(D)
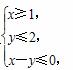 则x+y的最小值是______.
则x+y的最小值是______.