题目内容
设全集U=R,集合A={x||x+2|<|x-1|},B={x|
≥-1},求A∩B,A∪B.
| 2-5x |
| 2x+3 |
考点:交集及其运算,并集及其运算
专题:函数的性质及应用,不等式的解法及应用
分析:分别求解绝对值的不等式和分式不等式化简集合A,B,然后直接利用交集和并集运算求解.
解答:
解:由|x+2|<|x-1|,得x<-
.
∴A={x||x+2|<|x-1|}={x|x<-
},
由
≥-1,得
≥0,解得:-
<x≤
.
∴B={x|
≥-1}={x|-
<x≤
},
∴A∩B={x|-
<x<-
},
A∪B={x|x≤
}.
| 1 |
| 2 |
∴A={x||x+2|<|x-1|}={x|x<-
| 1 |
| 2 |
由
| 2-5x |
| 2x+3 |
| 2-5x+2x+3 |
| 2x+3 |
| 3 |
| 2 |
| 5 |
| 3 |
∴B={x|
| 2-5x |
| 2x+3 |
| 3 |
| 2 |
| 5 |
| 3 |
∴A∩B={x|-
| 3 |
| 2 |
| 1 |
| 2 |
A∪B={x|x≤
| 5 |
| 3 |
点评:本题考查了交集与并集运算,考查了绝对值不等式与分式不等式的解法,是基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
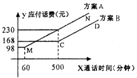 电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )| A、方案A | B、方案B |
| C、两种方案一样优惠 | D、不能确定 |