题目内容
 观察如图三角形数阵,则
观察如图三角形数阵,则(1)若记第n行的第m个数为anm,则a73=
(2)第n(n≥2)行的第2个数是
考点:归纳推理
专题:推理和证明
分析:由图可知,各行数字中除两端的数代表行数外,其他元素均等于上一行中其肩上的数的和,如4=2+2,7=3+4,11=7+4,14=7+7,据此规律进行求解.
解答:
解:(1)由图可知,各行数字中除两端的数代表行数外,其他元素均等于上一行中其肩上的数的和,
因此第6行的数为6,16,25,25,16,6
第7行的数为7,22,41,50,41,22,7
若记第n行的第m个数为anm,则a73=41.
(2)设n(n≥2)行的第2个数构成数列{an},
因为a3-a2=2,a4-a3=3,a5-a4=4,an-an-1=n-1
所以an-a2=2+3+4+…+(n-1)=
,又a2=2,
所以an=
.
故答案为:41,
因此第6行的数为6,16,25,25,16,6
第7行的数为7,22,41,50,41,22,7
若记第n行的第m个数为anm,则a73=41.
(2)设n(n≥2)行的第2个数构成数列{an},
因为a3-a2=2,a4-a3=3,a5-a4=4,an-an-1=n-1
所以an-a2=2+3+4+…+(n-1)=
| (n+1)(n-2) |
| 2 |
所以an=
| n2-n+2 |
| 2 |
故答案为:41,
点评:本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.此题要根据已知的数据发现各行的第一个数和第二个数的规律.

练习册系列答案
相关题目
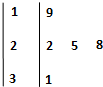 已知某篮球运动员2013年度参加了25场比赛,若从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为 ( )
已知某篮球运动员2013年度参加了25场比赛,若从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为 ( )| A、4 | ||
B、
| ||
| C、18 | ||
| D、16 |
函数y=x2+4x+7的图象按向量
经过一次平移后得到y=x2的图象,则
=( )
| a |
| a |
| A、(2,3) |
| B、(-2,3) |
| C、(-2,-3) |
| D、(2,-3) |
设有一个回归方程为
=2.5x+3,变量x增加一个单位时,则( )
 |
| y |
| A、y平均增加5.5个单位 |
| B、y平均增加2.5个单位 |
| C、y平均减少2.5个单位 |
| D、y平均减少5.5个单位 |
