题目内容
7.已知边长为2的正三角形ABC,P,M满足|AP|=1,$\overrightarrow{PM}$=$\overrightarrow{MC}$,则$\overrightarrow{BM}$2的最小值是( )| A. | $\frac{9-2\sqrt{3}}{4}$ | B. | $\frac{11-3\sqrt{3}}{4}$ | C. | $\frac{13-4\sqrt{3}}{4}$ | D. | $\frac{15-5\sqrt{3}}{4}$ |
分析 画出图形,建立坐标系,求出P的轨迹方程,由中点坐标公式和代入法求得M的轨迹方程,然后利用圆的性质|$\overrightarrow{BM}$2的最小值.
解答  解:由题△ABC为边长为2的正三角形,
解:由题△ABC为边长为2的正三角形,
如图建立平面坐标系,
可得A(0,$\sqrt{3}$),B(-1,0),C(1,0),
由|$\overrightarrow{AP}$|=1得点P的轨迹方程为x2+(y-$\sqrt{3}$)2=1,
设M(x0,y0),由$\overrightarrow{PM}$=$\overrightarrow{MC}$,得M为线段PC的中点,
则P(2x0-1,2y0),
代入①式得M的轨迹方程为(2x0-1)2+(2y0-$\sqrt{3}$)2=1,
即为((x0-$\frac{1}{2}$)2+(y0-$\frac{\sqrt{3}}{2}$)2=$\frac{1}{4}$,
记圆心为N($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),半径r=$\frac{1}{2}$,
|$\overrightarrow{BM}$|min=|$\overrightarrow{BN}$|-r=$\sqrt{(\frac{1}{2}+1)^{2}+(\frac{\sqrt{3}}{2})^{2}}$-$\frac{1}{2}$=$\sqrt{3}$-$\frac{1}{2}$,
则$\overrightarrow{BM}$2的最小值是$\frac{13-4\sqrt{3}}{4}$.
故选:C.
点评 本题考查向量平方的最小值的求法,圆方程的运用,向量的坐标运算,考查计算能力,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
9. 阅读右边的程序框图,运行相应的程序,输出k的值是( )
阅读右边的程序框图,运行相应的程序,输出k的值是( )
 阅读右边的程序框图,运行相应的程序,输出k的值是( )
阅读右边的程序框图,运行相应的程序,输出k的值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x≥1,}&{\;}\\{x+y≤4,}&{\;}\\{x+by-1≤0}&{\;}\end{array}\right.$且目标函数z=x+2y最小值为1,则实数b的取值范围是( )
| A. | (-∞,0) | B. | (-∞,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,0) | D. | (-∞,0)∪[2,+∞) |
16.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a(x-3)}\end{array}\right.$,若z=2x+y的最小值为1,则a=( )
| A. | 1 | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
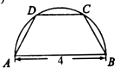 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.