题目内容
20．已知圆的一般方程为x2+y2-2x+4y+4=0．（1）写出该圆的圆心坐标和半径；
（2）求过该圆的圆心且倾斜角为$\frac{3π}{4}$的直线方程．
分析 （1）把所给的圆的一般方程化为标准方程，求出圆心坐标和半径．
（2）先求出直线的斜率为-1，再由点斜式求得要求直线的方程．
解答 解：（1）圆的一般方程为x2+y2-2x+4y+4=0，即 （x-1）2+（y+2）2 =1，
故圆心的坐标为（1，-2），半径为1．
（2）由题意可得所求的直线的斜率为tan$\frac{3π}{4}$=-1，由点斜式求得要求直线的方程为 y+2=-1（x-1），
即 x+y+1=0．
点评 本题主要考查圆的一般方程和标准方程，用点斜式求直线的方程，属于基础题．
练习册系列答案
相关题目
已知函数$f（x）=\left\{\begin{array}{l}x-1，x≥1\\-x+1，x＜1\end{array}\right.$．
11．“a≠2”是直线ax+2y=3与直线x+（a-1）y=1相交的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
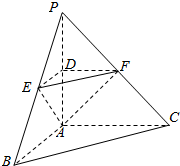如图，在三棱锥P-ABC中，平面PAC⊥平面ABC，PA⊥BC，AB⊥AC，PA=1，BC=2．D、E、F分别是棱PA、PB、PC的中点，连接DE、DF、EF．
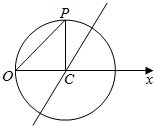在极坐标系中，已知圆C经过点P（$\sqrt{2}$，$\frac{π}{4}$），圆心为直线$ρsin（θ-\frac{π}{3}）$=-$\frac{\sqrt{3}}{2}$与极轴的交点，求圆C的直角坐标方程．
12．已知A，B分别为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右顶点，P是C上一点，且直线AP，BP的斜率之积为2，则C的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{5}$ | D． | $\sqrt{6}$ |