题目内容
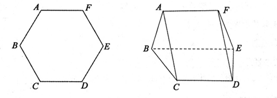
如图，正方体ABCD-A1B1C1D1的棱长为1，E为棱DD1上的点，F为AB的中点，则三棱锥B1-BFE的体积为考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：由VB1-BEF=VE-BB1F，利用等积法能求出三棱锥B1-BFE的体积．
解答：
解：∵正方体ABCD-A1B1C1D1的棱长为1，
E为棱DD1上的点，F为AB的中点，
∴三棱锥B1-BFE的体积：
VB1-BEF=VE-BB1F=
×AD×S△BB1F
=
×1×
×
×1=
．
故答案为：
．
解：∵正方体ABCD-A1B1C1D1的棱长为1，E为棱DD1上的点，F为AB的中点，
∴三棱锥B1-BFE的体积：
VB1-BEF=VE-BB1F=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
故答案为：
| 1 |
| 12 |
点评：本小题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．
练习册系列答案
阅读快车系列答案
相关题目
若
＜θ＜
，则下列不等式成立的是（ ）
| π |
| 4 |
| π |
| 3 |
| A、sinθ＞cosθ＞tanθ |
| B、cosθ＞tanθ＞sinθ |
| C、sinθ＞tanθ＞cosθ |
| D、tanθ＞sinθ＞cosθ |
设f（x）=x（x-1）（x-2）…（x-2015），则f′（2015）=（ ）
| A、-2013！ |
| B、-2015！ |
| C、2013！ |
| D、2015！ |
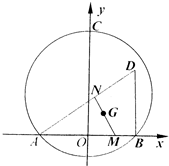在平面直角坐标系xOy中，已知点A（-1，0），B（1，0），C（0，a）（a∈R且a≠0），且动点D满足DA=