题目内容
已知a，b，c分别是△ABC三个内角A，B，C的对边，b=
，c=
，B=
，那么a等于（ ）
| 7 |
| 3 |
| π |
| 6 |
| A、1 | B、2 | C、4 | D、1或4 |
考点：余弦定理
专题：解三角形
分析：由余弦定理列出关系式，把b，c，cosB的值代入计算即可求出a的值．
解答：
解：∵△ABC中，b=
，c=
，cosB=
，
∴由余弦定理得：b2=a2+c2-2accosB，即7=a2+3-3a，
解得：a=4或a=-1（舍去），
则a的值为4．
故选：C．
| 7 |
| 3 |
| ||
| 2 |
∴由余弦定理得：b2=a2+c2-2accosB，即7=a2+3-3a，
解得：a=4或a=-1（舍去），
则a的值为4．
故选：C．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
设i是虚数单位，若复数x满足x（1-i）=i，则其虚部为（ ）
A、
| ||
B、-
| ||
C、-
| ||
D、
|
“手持技术和数学学科整合”是十二五重点研究课题，某县为调查研究数学教师在教学中手持技术的使用情况，采用简单随机抽样的方法，从该县180名授课教师中抽取20名教师，调查他们在上学期的教学中使用手持技术的次数，结果用茎叶图表示，则据此可估计上学期180名教师中使用次数落在[15，25）的人数为
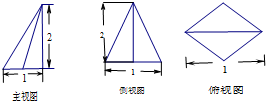一个几何体的三视图及部分数据如图所示，侧视图为等腰三角形，俯视图为正方形，则这个几何体的体积为（ ）A、
| ||
B、
| ||
| C、1 | ||
D、
|