题目内容
已知数列{an}中,a1=3,a2=5,其前n项和Sn满足Sn+Sn-2=2Sn-1+2n-1(n≥3).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ) 若bn=log2(
)n∈N*,设数列{bn}的前n的和为Sn,当n为何值时,Sn有最大值,并求最大值.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ) 若bn=log2(
| 256 |
| a2n-1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由Sn-Sn-1=Sn-1-Sn-2+2n-1(n≥3)得an=an-1+2n-1(n≥3),利用累加法及等比数列求和公式即可求得结论;
(Ⅱ)由bn=log2(
)n∈N*得bn=log2(
)=log2
=log228-2n=8-2n(n∈N*),判断bn的符号即可得出结论.
(Ⅱ)由bn=log2(
| 256 |
| a2n-1 |
| 256 |
| a2n-1 |
| 28 |
| 22n |
解答:
解:(Ⅰ)由题意知Sn-Sn-1=Sn-1-Sn-2+2n-1(n≥3),
即an=an-1+2n-1(n≥3)…(3分)
∴an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+a2=2n-1+2n-2+…+22+5…(5分)
=2n-1+2n-2+…+22+2+1+2=2n+1(n≥3),…(7分)
检验知n=1,2时,结论也成立,故an=2n+1.…(8分)
(Ⅱ) 由bn=log2(
)=log2
=log228-2n=8-2n(n∈N*)…(10分)
当1≤n≤3时,bn=8-2n>0;当n=4时,bn=8-2n=0;当n≥5时,bn=8-2n<0…(12分)
故n=3或n=4时,Sn达最大值,S3=S4=12.…(14分)
即an=an-1+2n-1(n≥3)…(3分)
∴an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+a2=2n-1+2n-2+…+22+5…(5分)
=2n-1+2n-2+…+22+2+1+2=2n+1(n≥3),…(7分)
检验知n=1,2时,结论也成立,故an=2n+1.…(8分)
(Ⅱ) 由bn=log2(
| 256 |
| a2n-1 |
| 28 |
| 22n |
当1≤n≤3时,bn=8-2n>0;当n=4时,bn=8-2n=0;当n≥5时,bn=8-2n<0…(12分)
故n=3或n=4时,Sn达最大值,S3=S4=12.…(14分)
点评:本题主要考查利用累加法求数列的通项公式及等差数列前n项和最值的求法等知识,属中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
数列{an}的通项公式为an=(
)2n-4-(
)n-2,则数列{an}( )
| 4 |
| 5 |
| 4 |
| 5 |
| A、有最大项,无最小项 |
| B、有最小项,无最大项 |
| C、既有最大项又有最小项 |
| D、既无最大项又无最小项 |
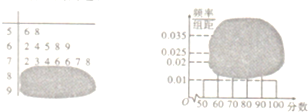 某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏,其可见部分信息如图所示,据此解答下列问题;
某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏,其可见部分信息如图所示,据此解答下列问题;