题目内容
如图所示,正方体ABCDA1B1C1D1中,A1C与截面DBC1交于O点,AC,BD交于M点,求证:C1,O,M三点共线.

证明:因为C1∈平面A1ACC1,且C1∈平面DBC1,
所以C1是平面A1ACC1与平面DBC1的公共点.
又因为M∈AC,所以M∈平面A1ACC1.
因为M∈BD,所以M∈平面DBC1,
所以M也是平面A1ACC1与平面DBC1的公共点,
所以C1M是平面A1ACC1与平面DBC1的交线.
因为O为A1C与截面DBC1的交点,
所以O∈平面A1ACC1,O∈平面DBC1,
即O也是两平面的公共点,
所以O∈直线C1M,即C1,O,M三点共线.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 ,命题
,命题 ,命题
,命题 .
. 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围; 为真命题,命题
为真命题,命题 为假命题,求实数
为假命题,求实数 H必在( )
H必在( )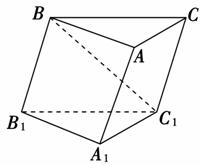
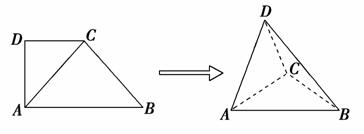
 序号是( )
序号是( )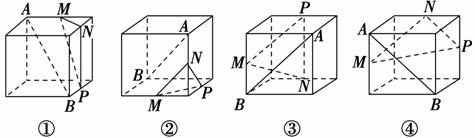
 C.②③ D.②④
C.②③ D.②④ D.五棱锥
D.五棱锥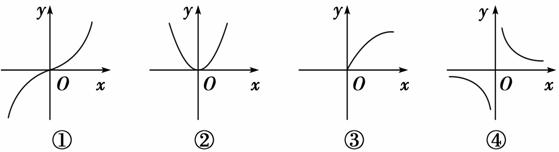
 ,②y=x2,③y=x
,②y=x2,③y=x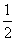 ,④y=x-1
,④y=x-1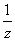 -
-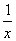 =
=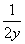 ;
;