题目内容
如图,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC,如图所示.
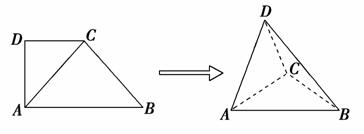
(1)求证:BC⊥平面ACD;
(2)求几何体DABC的体积.
 (1)证明:在平面图中,可得AC=BC=2
(1)证明:在平面图中,可得AC=BC=2 ,从而AC2+B
,从而AC2+B C2=AB2,故AC⊥BC.取AC的中点O,连接DO,则
C2=AB2,故AC⊥BC.取AC的中点O,连接DO,则 DO⊥AC.又平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,DO⊂平面ADC,从而DO⊥平面ABC,∴DO⊥BC.
DO⊥AC.又平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,DO⊂平面ADC,从而DO⊥平面ABC,∴DO⊥BC.
又AC⊥BC,AC∩DO=O,∴ BC⊥平面ACD.
BC⊥平面ACD.
(2)解析:由(1)可知BC为三棱锥BACD的高,BC=2 ,S△ACD=2,∴VBACD=
,S△ACD=2,∴VBACD= S△
S△ ACD·BC=
ACD·BC= ×2×2
×2×2 =
= .
.
由等体积性可知,几何体DABC的体积为 .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足;
满足; ;(ii)对任意
;(ii)对任意 ,当
,当 时,恒有
时,恒有 .
. ;
; ;
; ;
;
 与前面的三角形面垂直,则该几何体的左视图为( )
与前面的三角形面垂直,则该几何体的左视图为( ) 

 的正方形,侧棱D1D垂直于底面ABCD,且D1D=3.
的正方形,侧棱D1D垂直于底面ABCD,且D1D=3. =1,求证:A1P⊥平面PBD;
=1,求证:A1P⊥平面PBD;

 B.200+18π
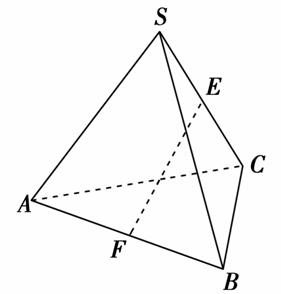
B.200+18π 为a的正三角形,E,F分别是SC和AB的中点,则异面直线EF与SA所成的角等于 (
为a的正三角形,E,F分别是SC和AB的中点,则异面直线EF与SA所成的角等于 (  )
) 
 B.60°
B.60°
 ,则这个圆锥的母线长为( )
,则这个圆锥的母线长为( )