Question

设x，y，z∈R_＋，且3^x＝4^y＝6^z.

(1)求证：－＝；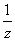

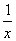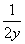(2)比较3x,4y,6z的大小．

Answer 1

证明：设3^x＝4^y＝6^z＝k，

因为x，y，z∈R_＋，所以k＞1，x＝log₃k，y＝log₄k，z＝log₆k.

(1)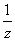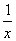－＝－＝log_k6－log_k3＝log_k2

＝log_k4＝＝.

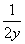即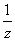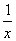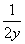－＝成立．

(2)解析：因为k＞1，所以lg k＞0,

所以3x－4y＝ (lg 64－lg 81)＜0，

4y－6z＝ (lg 36－lg 64)＜0，

所以3x＜4y＜6z.