题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}sin({x+α}),({x≤0})\\ cos({x-β}),({x>0})\end{array}$是偶函数,则下列结论可能成立的是( )| A. | $α=\frac{π}{4},β=\frac{π}{8}$ | B. | $α=\frac{2π}{3},β=\frac{π}{6}$ | C. | $α=\frac{π}{3},β=\frac{π}{6}$ | D. | $α=\frac{5π}{6},β=\frac{2π}{3}$ |
分析 根据题意,由偶函数的性质可得sin(x+α)=cos(-x-β),进而利用三角函数的和差公式化简可得sinxcosα+cosxsinα=cosxcosβ-sinxsinβ,分析可得sinα=cosβ,cosα=-sinβ,由三角函数诱导公式分析可得α=β+$\frac{π}{2}$,分析选项即可得答案.
解答 解:根据题意,设x>0,则-x<0,
则有f(x)=sin(x+α),f(-x)=cos(-x-β),
又由函数f(x)是偶函数,则有sin(x+α)=cos(-x-β),
变形可得:sin(x+α)=cos(x+β),
即sinxcosα+cosxsinα=cosxcosβ-sinxsinβ,
必有:sinα=cosβ,cosα=-sinβ,
分析可得:α=β+$\frac{π}{2}$,
分析选项只有B满足α=β+$\frac{π}{2}$,
故选:B.
点评 本题考查偶函数的性质,涉及三角函数和差公式的应用,关键是利用偶函数的性质,得到关于α、β的三角恒等式.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
8.直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,BC=2$\sqrt{2}$,则三棱柱ABC-A1B1C1的外接球的表面积为( )
| A. | 36π | B. | 28π | C. | 16π | D. | 12π |
10.已知等比数列{an}的公比为正数,前n项和为Sn,a1+a2=2,a3+a4=6,则S8等于( )
| A. | $81-27\sqrt{3}$ | B. | 54 | C. | 38-1 | D. | 80 |
7.已知集合A={x∈N|0≤x≤5},B={x|2-x<0},则A∩(∁RB)=( )
| A. | {1} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
14.若$f(x)=cos2x+acos({\frac{π}{2}+x})$在区间$({\frac{π}{6},\frac{π}{2}})$上是增函数,则实数a的取值范围为( )
| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-∞,-4) | D. | (-∞,-4] |
12.已知α是第一象限角,满足$sinα-cosα=\frac{{\sqrt{10}}}{5}$,则cos2α=( )
| A. | -$\frac{3}{5}$ | B. | $±\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $±\frac{4}{5}$ |
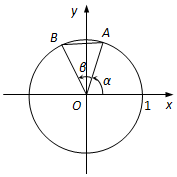 如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB=$\frac{{2\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB=$\frac{{2\sqrt{5}}}{5}$.