题目内容
为测量某塔AB的高度，在一幢与塔AB相距20m的楼顶处测得塔顶A的仰角为30°，测得塔基B的俯角为45°，那么塔AB的高度是（ ）
A、20（1+
| ||||
B、20（1+
| ||||
C、20（1+
| ||||
D、20（1-
|
考点：解三角形的实际应用
专题：计算题,解三角形
分析：设观测点为C，CP为点C与塔AB的距离，可得∠ACP=30°且∠BCP=45°．利用直角三角形中的三角函数的定义求得AP、CP的值，即可求得塔高AB的值．
解答：
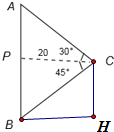解：如图所示，设观测点为C，CP=20为点C与塔AB的距离，
∠ACP=30°，∠BCP=45°．
则AB=AP+CP=PC•tan30°+CP•tan45°
=20×
+20×1=20（1+
），
即塔AB的高度是20（1+
）m，
故选：A．
解：如图所示，设观测点为C，CP=20为点C与塔AB的距离，∠ACP=30°，∠BCP=45°．
则AB=AP+CP=PC•tan30°+CP•tan45°
=20×
| ||
| 3 |
| ||
| 3 |
即塔AB的高度是20（1+
| ||
| 3 |
故选：A．
点评：本题给出实际应用问题，求塔AB的高度．着重考查了直角三角形中三角函数的定义和解三角形在实际生活中的应用等知识，属于基础题．
练习册系列答案
百分学生作业本题练王系列答案
相关题目
对于函数f（x），若存在区间M=[a，b]，（a＜b），使得{y|y=f（x），x∈M}=M，则称区间M为函数f（x）的一个“稳定区间”．下列所给出的函数中不存在“稳定区间”的是（ ）
| A、f（x）=ex | ||
| B、f（x）=x2 | ||
C、f（x）=cos
| ||
| D、f（x）=x |