题目内容
若命题p:-2<
<2,命题q:集合A={x|x2+(a+2)x+1=0,x∈R}有两个不同元素,求使命题p,q中有且只有一个真命题时,实数a的取值范围.
| 1-a |
| 3 |
考点:复合命题的真假
专题:简易逻辑
分析:对于命题p:-2<
<2,解得-5<a<7.命题q:集合A={x|x2+(a+2)x+1=0,x∈R}有两个不同元素,△>0,解得a<-4或a>0.由于命题p,q中有且只有一个真命题,解出即可.
| 1-a |
| 3 |
解答:
解:命题p:-2<
<2,命题p为真命题时,解得-5<a<7.
命题q:集合A={x|x2+(a+2)x+1=0,x∈R}有两个不同元素,命题q为真命题时,△=(a+2)2-4>0,解得a<-4或a>0.
若p真q假,则
,得-4≤a≤0.
若p假q真,则
,得a≤-5或a≥7.
综上,a的取值范围为(-∞,-5]∪[-4,0]∪[7,+∞).
| 1-a |
| 3 |
命题q:集合A={x|x2+(a+2)x+1=0,x∈R}有两个不同元素,命题q为真命题时,△=(a+2)2-4>0,解得a<-4或a>0.
若p真q假,则
|
若p假q真,则
|
综上,a的取值范围为(-∞,-5]∪[-4,0]∪[7,+∞).
点评:本题考查了一元二次不等式的解法与判别式的关系、不等式的解法、简易逻辑的判定,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
 如图所示,为测一建筑物的高度,在地面上选取A,B两点,从A,B两点分别测得建筑物顶端的仰角为30°,45°,且A,B两点间的距离为60m,则该建筑物的高度为( )
如图所示,为测一建筑物的高度,在地面上选取A,B两点,从A,B两点分别测得建筑物顶端的仰角为30°,45°,且A,B两点间的距离为60m,则该建筑物的高度为( )A、(30+30
| ||
B、(30+15
| ||
C、(15+30
| ||
D、(15+15
|
为测量某塔AB的高度,在一幢与塔AB相距20m的楼顶处测得塔顶A的仰角为30°,测得塔基B的俯角为45°,那么塔AB的高度是( )
A、20(1+
| ||||
B、20(1+
| ||||
C、20(1+
| ||||
D、20(1-
|
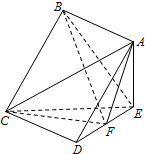 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.