题目内容
1．在△ABC中，已知a=2，A=45°，B=120°，则b=（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{6}$ | D． | $2\sqrt{2}$ |
分析 由已知利用正弦定理即可求值．
解答 解：∵a=2，A=45°，B=120°，
∴由正弦定理可得：b=$\frac{asinB}{sinA}$=$\frac{2×\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}$=$\sqrt{6}$．
故选：C．
点评 本题主要考查了正弦定理在解三角形中的应用，属于基础题．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
16．
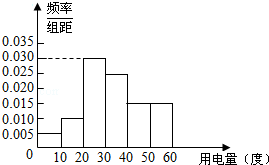某市政府为了确定一个较为合理的居民用电标准，必须先了解全市居民日常用电量的分布情况．现采用抽样调查的方式，获得了n位居民在2012年的月均用电量（单位：度）数据，样本统计结果如下图表：
（1）求月均用电量的中位数与平均数估计值；
（2）如果用分层抽样的方法从这n位居民中抽取8位居民，再从这8位居民中选2位居民，那么至少有1位居民月均用电量在30至40度的概率是多少？
（3）用样本估计总体，把频率视为概率，从这个城市随机抽取3位居民（看作有放回的抽样），求月均用电量在30至40度的居民数X的分布列．
某市政府为了确定一个较为合理的居民用电标准，必须先了解全市居民日常用电量的分布情况．现采用抽样调查的方式，获得了n位居民在2012年的月均用电量（单位：度）数据，样本统计结果如下图表：| 分 组 | 频 数 | 频 率 |
| [0，10） | 0.05 | |
| [10，20） | 0.10 | |
| [20，30） | 30 | |
| [30，40） | 0.25 | |
| [40，50） | 0.15 | |
| [50，60] | 15 | |
| 合 计 | n | 1 |
（2）如果用分层抽样的方法从这n位居民中抽取8位居民，再从这8位居民中选2位居民，那么至少有1位居民月均用电量在30至40度的概率是多少？
（3）用样本估计总体，把频率视为概率，从这个城市随机抽取3位居民（看作有放回的抽样），求月均用电量在30至40度的居民数X的分布列．
10．已知定义在R上的奇函数f（x）满足f（x+2）=f（x），且在（0，1]上，满足f（x）=$\frac{x^2-x}{2}$，则f（-2016）+f（-2016$\frac{1}{2}$）=（ ）
| A． | 0 | B． | $\frac{1}{4}$ | C． | -$\frac{1}{8}$ | D． | $\frac{1}{8}$ |