题目内容
 如图,设G为△ABO的重心,过G的直线与边OA、OB分别交于P和Q,已知
如图,设G为△ABO的重心,过G的直线与边OA、OB分别交于P和Q,已知| OP |
| OA |
| OQ |
| OB |
(1)求函数y=f(x)的解析式;
(2)求
| T |
| S |
考点:平面向量数量积的运算,函数解析式的求解及常用方法,平面向量的坐标运算
专题:平面向量及应用
分析:(1)由中心可得
=
(
+
),进而可得
和
,由
与
共线,
与
不共线可得
=
变形即可;(2)分别可得S和T,可得
=xy=
=
,令g(x)=
-
=-(
-
)2+
,由二次函数区间的最值可得.
| OG |
| 1 |
| 3 |
| OA |
| OB |
| GP |
| QG |
| GP |
| QG |
| OA |
| OB |
x-
| ||
|
-
| ||
|
| T |
| S |
| x2 |
| 3x-1 |
| 1 | ||||
|
| 3 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 3 |
| 2 |
| 9 |
| 4 |
解答:
解:(1)∵
=
=
×
(
+
)=
(
+
),
=
-
=x
-
(
+
)=(x-
)
-
,
=
-
=
(
+
)-y
=
+(
-y)
,
∵
与
共线,
与
不共线,
∴
=
变形可得y=
(
≤x≤1)即为所求.
(2)∵T=
|
|×|
sin∠BOA=
xy|
|×|
sin∠BOA,
S=
|
|×|
sin∠BOA,
∴
=xy=
=
,
令g(x)=
-
=-(
-
)2+
,
∵
≤x≤1,∴1≤
≤2,
当
=
时,g(x)取最大值
,
当
=1或2时,g(x)取最小值2,
∴
的取值范围为[
,
].
| OG |
| 2 |
| 3 |
| OM |
| 2 |
| 3 |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 3 |
| OA |
| OB |
| GP |
| OP |
| OG |
| OA |
| 1 |
| 3 |
| OA |
| OB |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| QG |
| OG |
| OQ |
| 1 |
| 3 |
| OA |
| OB |
| OB |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
∵
| GP |
| QG |
| OA |
| OB |
∴
x-
| ||
|
-
| ||
|
| x |
| 3x-1 |
| 1 |
| 2 |
(2)∵T=
| 1 |
| 2 |
| OP |
| OQ| |
| 1 |
| 2 |
| OA |
| OB| |
S=
| 1 |
| 2 |
| OA |
| OB| |
∴
| T |
| S |
| x2 |
| 3x-1 |
| 1 | ||||
|
令g(x)=
| 3 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 3 |
| 2 |
| 9 |
| 4 |
∵
| 1 |
| 2 |
| 1 |
| x |
当
| 1 |
| x |
| 3 |
| 2 |
| 9 |
| 4 |
当
| 1 |
| x |
∴
| T |
| S |
| 4 |
| 9 |
| 1 |
| 2 |
点评:本题考查平面向量的数量积,涉及二次函数区间的最值,属基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
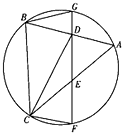 如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD.
如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD. 如图甲,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD,E、F、G分别是PC、PD、BC的中点,现将△PDC沿CD折起,使平面PDC⊥平面ABCD(如图乙),且所得到的四棱锥P-ABCD的正视图、侧视图、俯视图的面积总和为8.
如图甲,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD,E、F、G分别是PC、PD、BC的中点,现将△PDC沿CD折起,使平面PDC⊥平面ABCD(如图乙),且所得到的四棱锥P-ABCD的正视图、侧视图、俯视图的面积总和为8. 如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明.
如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明.