题目内容
若实数m满足0＜m＜8，则曲线C1：
-
=1与曲线C2：
-
=1的（ ）
| x2 |
| 24 |
| y2 |
| 8-m |
| x2 |
| 24-m |
| y2 |
| 8 |
| A、焦距相等 |
| B、实半轴长相等 |
| C、虚半轴长相等 |
| D、离心率相等 |
考点：双曲线的标准方程
专题：圆锥曲线的定义、性质与方程
分析：根据m的取值范围，判断曲线为对应的双曲线，以及a，b，c的大小关系即可得到结论．
解答：
解：当0＜m＜8，则0＜8-m＜8，16＜24-m＜24，
即曲线C1：
-
=1表示焦点在x轴上的双曲线，其中a2=24，b2=8-m，c2=32-m，
曲线C2：
-
=1表示焦点在x轴上的双曲线，其中a′2=24-m，b′2=8，c′2=32-m，
即两个双曲线的焦距相等，
故选：A．
即曲线C1：
| x2 |
| 24 |
| y2 |
| 8-m |
曲线C2：
| x2 |
| 24-m |
| y2 |
| 8 |
即两个双曲线的焦距相等，
故选：A．
点评：本题主要考查双曲线的方程和性质，根据不等式的范围判断a，b，c是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
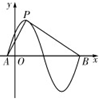函数y=sin（πx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高点，A，B是图象与x轴的交点，把∠APB=θ，则tanθ的值是（ ）