题目内容
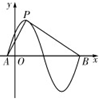 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,把∠APB=θ,则tanθ的值是( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,把∠APB=θ,则tanθ的值是( )| A、8 | ||
B、
| ||
C、
| ||
D、
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由题意求出函数的周期与最值,过点P作PD⊥x轴于D,解出∠APD与∠BPD的正切值,利用两角和的正切函数求出tanθ.
解答:
 解:由题意可知T=
解:由题意可知T=
=2,最大值为1;
过P作PD⊥x轴于D,
则AD=
=
,DB=
,DP=1,
所以tan∠APD=
与tan∠BPD=
,
所以tanθ=tan(∠APD+∠BPD)=
=8.
故选:A.
 解:由题意可知T=
解:由题意可知T=| 2π |
| π |
过P作PD⊥x轴于D,
则AD=
| T |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
所以tan∠APD=
| 1 |
| 2 |
| 3 |
| 2 |
所以tanθ=tan(∠APD+∠BPD)=
| ||||
1-
|
故选:A.
点评:本题考查三角函数的图象与两角和的正切函数公式的应用,题目新,考查理解能力、计算能力.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
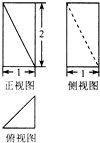
如图是某几何体的三视图,则该几何体的体积等于( )

A、
| ||
B、
| ||
| C、1 | ||
D、
|
设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)-lnx]=e+1,若x0是方程f(x)-f′(x)=e的一个解,则x0可能存在的区间是( )
| A、(0,1) |
| B、(e-1,1) |
| C、(0,e-1) |
| D、(1,e) |
若实数m满足0<m<8,则曲线C1:
-
=1与曲线C2:
-
=1的( )
| x2 |
| 24 |
| y2 |
| 8-m |
| x2 |
| 24-m |
| y2 |
| 8 |
| A、焦距相等 |
| B、实半轴长相等 |
| C、虚半轴长相等 |
| D、离心率相等 |
在平面直角坐标系xOy中,已知角α的顶点与点O重合,始边与x轴的非负半轴重合,终边上一点M的坐标为(
,1),则cos(α+
)的值是( )
| 3 |
| π |
| 3 |
| A、-0.5 | B、0 | C、0.5 | D、1 |