题目内容
已知a是实数，函数f（x）=ax2+2x-1，如果函数y=f（x）在区间[-1，1]上有零点，求a的取值范围．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：函数的零点，即为ax2+2x-1=0的根，当a=0时，显然不成立，因此可化为a=
，x∈[-1，1]的值域问题．
| 1-2x |
| x2 |
解答：
解：由题意得ax2+2x-1=0在区间[-1，1]上有解，
当x=0时，-1=0显然不成立
当x≠0时，原方程可化为a=(
)2-2•
=(
-1)2-1，
∈(-∞，-1)∪（1，+∞）．
显然a＞-1．
故所求a的范围是（-1，+∞）．
当x=0时，-1=0显然不成立
当x≠0时，原方程可化为a=(
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
显然a＞-1．
故所求a的范围是（-1，+∞）．
点评：本题考查了函数零点的概念以及利用函数思想解决方程根的存在性问题．
练习册系列答案
相关题目
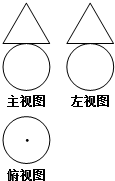某几何体三视图如图所示，其中三角形的三边长与圆的直径均为2，则该几何体体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若实数m满足0＜m＜8，则曲线C1：
-
=1与曲线C2：
-
=1的（ ）
| x2 |
| 24 |
| y2 |
| 8-m |
| x2 |
| 24-m |
| y2 |
| 8 |
| A、焦距相等 |
| B、实半轴长相等 |
| C、虚半轴长相等 |
| D、离心率相等 |