题目内容
5.在直三棱柱ABC-A1B1C1中,侧棱长为$2\sqrt{3}$,在底面△ABC中,∠C=60°,$AB=\sqrt{3}$,则此直三棱柱的外接球的表面积为( )| A. | $4\sqrt{3}π$ | B. | $\frac{16π}{3}$ | C. | 16π | D. | $\frac{32π}{3}$ |
分析 由题意可知直三棱柱ABC-A1B1C1中,底面ABC的小圆半径为1,连接两个底面中心的连线,中点与顶点的连线就是球的半径,即可求出球的表面积.
解答 解:由题意可知直三棱柱ABC-A1B1C1中,底面小圆ABC的半径为$\frac{\sqrt{3}}{2•\frac{\sqrt{3}}{2}}$=1,
连接两个底面中心的连线,中点与顶点的连线就是球的半径,外接球的半径为:$\sqrt{3+1}$=2,
外接球的表面积为:4π•22=16π.
故选C.
点评 本题是中档题,考查直三棱柱的外接球的表面积的求法,解题的关键是外接球的半径,直三棱柱的底面中心的连线的中点与顶点的连线是半径,考查空间想象能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.集合P={x|x<2},集合Q={y|y<1},则P与Q的关系为( )
| A. | P⊆Q | B. | Q⊆P | C. | P=Q | D. | 以上都不正确 |
9.设$0<a<\frac{1}{3}$,r=aa,$s={log_{\frac{1}{3}}}a$,$t={a^{\frac{1}{3}}}$,则( )
| A. | r>s>t | B. | r>t>s | C. | s>r>t | D. | s>t>r |
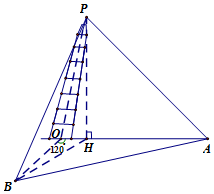 上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求:
上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求: