题目内容
6.已知x,y∈R+,且x+2y=1,则x•y的最大值为$\frac{1}{8}$.分析 直接利用基本不等式的性质即可得出.
解答 解:x,y∈R+,
x+2y=1,即1$≥2\sqrt{2xy}$,当且仅当x=2y=$\frac{1}{2}$时取等号.
那么:$\frac{1}{4}≥2xy$,
可得:xy$≤\frac{1}{8}$.
∴x•y的最大值为$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题考查了基本不等式的性质的运用,属于基础题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
16.下列以x为自变量的函数中,是指数函数的是( )
| A. | $\begin{array}{l}\\ y={3^x}\end{array}$ | B. | y=(-3)x | C. | y=2x+1 | D. | y=x3 |
17.某奶茶店的日销售收入y(单位:百元)与当天平均气温x(单位:℃)之间的关系如下:
通过上面的五组数据得到了x与y之间的线性回归方程:$\stackrel{∧}{y}$=-x+2.8;但现在丢失了一个数据,该数据应为( )
| x | -2 | -1 | 0 | 1 | 2 |
| y | 5 | 2 | 2 | 1 |
| A. | 3 | B. | 4 | C. | 5 | D. | 2 |
14.设a∈R,则“a=1”是“复数(a-1)(a+2)+(a+3)i为纯虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
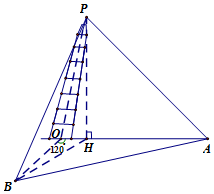 上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求:
上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求: