题目内容
 如图是一个封闭几何体的三视图,则该几何体的表面积为( )
如图是一个封闭几何体的三视图,则该几何体的表面积为( )| A、7πcm2 |
| B、8πcm2 |
| C、9πcm2 |
| D、11πcm2 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图可知:该几何体是一个圆柱挖去一个半球所得的组合体,分别计算各个面的面积,累加可得答案.
解答:
解:由已知中的三视图可知:该几何体是一个圆柱挖去一个半球所得的组合体,
圆柱的底面直径与半球的直径均为2,
圆柱的高为3,
故圆柱的底面面积为π×(
)2=π,
圆柱的侧面积为:2×π×3=6π,
半球面面积为:
×4×π×(
)2=2π,
故该几何体的表面积S=π+6π+2π=9π,
故选C
圆柱的底面直径与半球的直径均为2,
圆柱的高为3,
故圆柱的底面面积为π×(
| 2 |
| 2 |
圆柱的侧面积为:2×π×3=6π,
半球面面积为:
| 1 |
| 2 |
| 2 |
| 2 |
故该几何体的表面积S=π+6π+2π=9π,
故选C
点评:本题考查的知识点是由三视图求表面积,其中分析出几何体的形状是解答的关键.

练习册系列答案
相关题目
已知a=2ln3,b=2lg2,c=(
) log
,则( )
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、c>a>b |
| B、a>b>c |
| C、a>c>b |
| D、b>c>a |
y=f(x)满足2f(x)+f(
)=lnx,则函数f(x)在x=1处的切线斜率为( )
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
等差数列{an}中,a2=2007,a9=a5-12,则其前n项和Sn取最大值时n等于( )
| A、670 |
| B、671 |
| C、670或671 |
| D、671或672 |
△ABC中,若sinB•cosA<0,则三角形的形状为( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰直角三角形 |
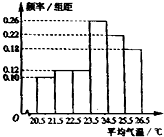 如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为( )
如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为( )