题目内容
在锐角△ABC中，a=3，b=4，S△ABC=3
，则角C= ．
| 3 |
考点：正弦定理
专题：解三角形
分析：利用三角形面积公式求得sinC，进而求得C．
解答：
解：∵S△ABC=
a•b•sinC=
•3•4•sinC=3
，
∴sinC=
，
∵△ABC为锐角三角形，
∴C=
．
故答案为：
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴sinC=
| ||
| 2 |
∵△ABC为锐角三角形，
∴C=
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题主要考查正弦定理的应用．考查了正弦定理公式及变形公式掌握．
练习册系列答案
相关题目
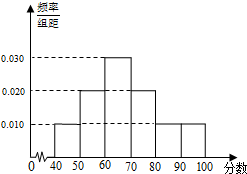某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计，得到如图所示的样本频率分布直方图．若规定60分及以上为合格，则估计这1000名学生中合格人数是
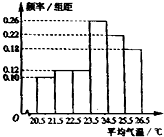如图是根据部分城市某年6月份的平均气温（单位：℃）数据得到的样本频率分布直方图，其中平均气温的范围是[20.5，26.5]，样本数据的分组为[20.5，21.5），[21.5，22.5），[22.5，23.5），[23.5，24.5），[24.5，25.5），[25.5，26.5]．已知样本中平均气温低于22.5℃的城市个数为11，则样本中平均气温不低于25.5℃的城市个数为（ ）△ABC中，若sinB•cosA＜0，则三角形的形状为（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰直角三角形 |